
数据预处理(Data Preprocessing)
零均值化(Mean subtraction)
为什么要零均值化?
人们对图像信息的摄取通常不是来自于像素色值的高低,而是来自于像素之间的相对色差。零均值化并没有消除像素之间的相对差异(交流信息),仅仅是去掉了直流信息的影响。
数据有过大的均值也可能导致参数的梯度过大。
如果有后续的处理,可能要求数据零均值,比如PCA。
假设数据存放在一个矩阵 X 中,X 的形状为(N,D),N 是样本个数,D 是样本维度,零均值化操作可用 python 的 numpy 来实现:
X -= numpy.mean(X, axis=0)
即 X 的每一列都减去该列的均值。
对于灰度图像,也可以减去整张图片的均值:
X -= numpy.mean(X)
对于彩色图像,将以上操作在3个颜色通道内分别进行即可。
归一化(Normalization)
为什么要归一化?
归一化是为了让不同纬度的数据具有相同的分布规模。
假如二维数据数据(x1,x2)两个维度都服从均值为零的正态分布,但是x1方差为100,x2方差为1。可以想像对(x1,x2)进行随机采样并在而为坐标系中标记后的图像,应该是一个非常狭长的椭圆形。
对这些数据做特征提取会用到以下形式的表达式:
S = w1*x1 + w2*x2 + b
那么:
dS / dw1 = x1
dS / dw2 = x2
由于x1与x2在分布规模上的巨大差异,w1与w2的导数也会差异巨大。此时绘制目标函数(不是S)的曲面图,就像一个深邃的峡谷,沿着峡谷方向变化的是w2,坡度很小;在峡谷垂直方向变化的是w1,坡度非常陡峭。
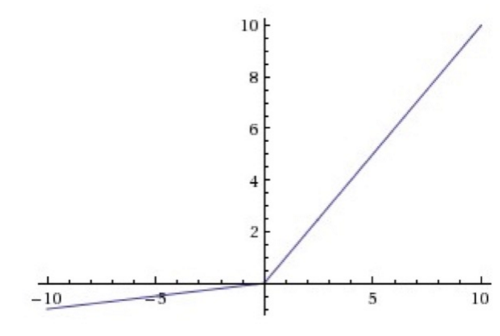
因为我们期望的目标函数是这样的:

而现在的目标函数可能是这样的:

我们知道这样的目标函数是非常难以优化的。因为w1与w2的梯度差异太大,在两个维度上需要不同的迭代方案。但是在实际操作中,为了简便,我们通常为所有维度设置相同的步长,随着迭代的进行,步长的缩减在不同维度间也是同步的。这就要求W不同维度的分布规模大致相同,而这一切都始于数据的归一化。
一个典型的归一化实现:
X /= numpy.std(X, axis = 0)
在自然图像上进行训练时,可以不进行归一化操作,因为(理论上)图像任一部分的统计性质都应该和其它部分相同,图像的这种特性被称作平稳性(stationarity)。(注意是同分布,不是独立同分布)
PCA & Whitening

白化相当于在零均值化与归一化操作之间插入一个旋转操作,将数据投影在主轴上。一张图片在经过白化后,可以认为各个像素之间是统计独立的。
然而白化很少在卷积神经网络中使用。我猜测是因为图像信息本来就是依靠像素之间的相对差异来体现的,白化让像素间去相关,让这种差异变得不确定,抹掉了很多信息。
数据扩充(Data Augmentation)
大型模型往往需要大量数据来训练。一些数据扩充方法因此被发明出来,以自然图像为例:



可以对图片做水平翻转、进行一定程度的位移或者剪裁,还可以对它的颜色做一定程度的调整。在不改变图像类别的情况下,增加数据量,还能提高模型的泛化能力。
参数初始化
零初始化
不要将参数全部初始化为零。
几乎所有的CNN网络都是对称结构,将参数零初始化会导致流过网络的数据也是对称的(都是零),并且没有办法在不受扰动的情况下打破这种数据对称,从而导致网络无法学习。
随机初始化
打破对称性的思路很简单,给每个参数随机赋予一个接近零的值就好了:
W = 0.01* numpy.random.randn(D,H)
randn 方法生成一个均值为零,方差为1的服从正态分布的随机数。
把 W 应用到之前的表达式 S ,S 就是多个随机变量的加权和。独立随机变量和的方差为:
Var(A+B+C) = Var(A)+Var(B)+Var(C)
假设 W 各元素之间相互独立,随着数据维度的增长,S 的方差将会线性累积。根据任务的不同,数据的维度从小到大跨度非常大,是不可控的,所以我们希望将 S 的方差做归一化,这只需要对 W 动动手脚就可以了:
W = numpy.random.randn(n) / sqrt(n)
其中 n 就是数据的维度。
推导过程如下:
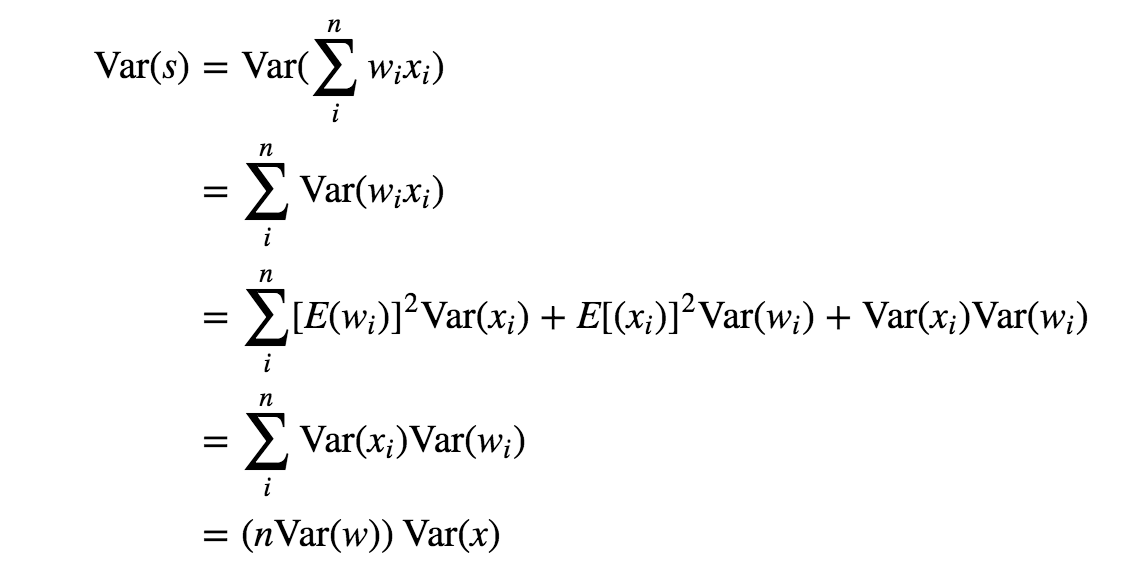
令 n*Var(W) = 1,就得到 std(W) = 1 / sqrt(n)。
在实际使用中,如果结合 ReLU,推荐:
w = numpy.random.randn(n) * sqrt(2.0/n)
激活函数(Activation Function)
激活函数用于在模型中引入非线性。
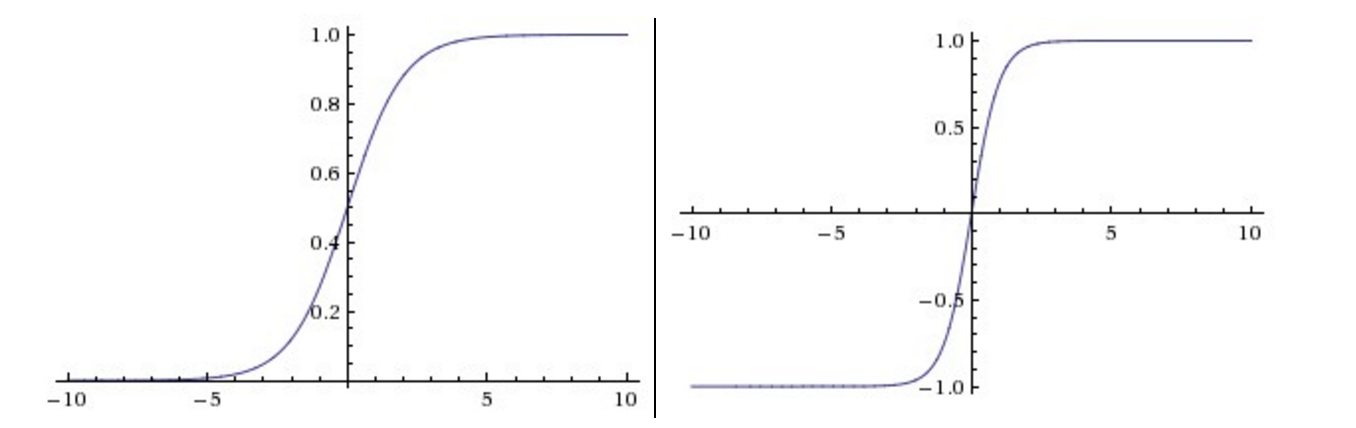
sigmoid 与 tanh 曾经很流行,但现在很少用于视觉模型了,主要原因在于当输入的绝对值较大时,其导数接近于零,梯度的反向传播过程将被中断,出现梯度消散的现象。
ReLU 是一个很好的替代:

相比于 sigmoid 与 tanh,它有两个优势:
没有饱和问题,大大缓解了梯度消散的现象,加快了收敛速度。
实现起来非常简单,加速了计算过程。
ReLU 有一个缺陷,就是它可能会永远“死”掉:
假如有一组二维数据 X(x1, x2)分布在 x1:[0,1], x2:[0,1] 的区域内,有一组参数 W(w1, w2)对 X 做线性变换,并将结果输入到 ReLU。
F = w1*x1 + w2*x2
如果 w1 = w2 = -1,那么无论 X 如何取值,F 必然小于等于零。那么 ReLU 函数对 F 的导数将永远为零。这个 ReLU 节点将永远不参与整个模型的学习过程。
造成上述现象的原因是 ReLU 在负区间的导数为零,为了解决这一问题,人们发明了 Leaky ReLU, Parametric ReLU, Randomized ReLU 等变体。他们的中心思想都是为 ReLU 函数在负区间赋予一定的斜率,从而让其导数不为零(这里设斜率为 alpha)。
Leaky ReLU 就是直接给 alpha 指定一个值,整个模型都用这个斜率:
Parametric ReLU 将 alpha 作为一个参数,通过学习获取它的最优值。Randomized ReLU 为 alpha 规定一个区间,然后在区间内随机选取 alpha 的值。
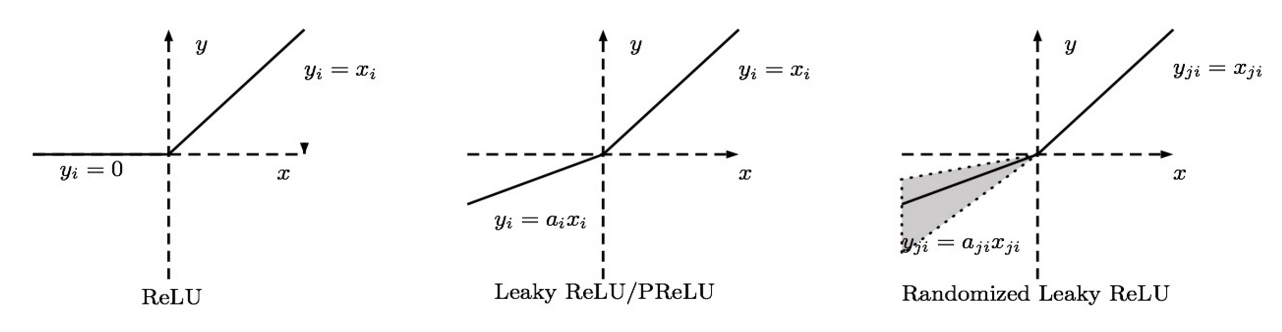
在实践中, Parametric ReLU 和 Randomized ReLU 都是可取的。
总结
仅仅理解 CNN 的结构是不够的,在实践中,特别是训练大规模网络的时候,有很多技巧性或经验性的细节。不仅要会用它们,更要理解这些技巧背后的规律。我认为合理的学习过程是:
实践-》总结-》再实践 循环往复
一开始看不懂论文,可以利用一些公开课或者教程,理解基本概念,并跟随教程完整的实现一些简单模型,找到最初始也是最重要的感觉。
然后总结在该领域内的一些最佳实践,并理解为什么这么做,渐渐对该领域形成体系化的认识。
在有了体系化的理解之后,你发现你有了举一反三的能力,可以尝试实现更复杂的模型,以印证自己的想法。还可以去阅读专业人士的论文,巩固和完善自己的认知体系。
此时你已经熬过了最痛苦的积累期,具有了创造的能力。关于CNN的细节,我还会再做补充讨论。